BLOQUE 4, RAZONES TRIGONOMETRICAS

RAZONES TRIGONOMETRICAS

RAZONES TRIGOMETRICAS 

DE ANGULOS AGUDOS

Son relaciones que se establecen entre los lados de un triángulo rectángulo.

Las razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad).

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométrica mente o por medio de sus relaciones.

Ejercicio 01:

En un triángulo rectángulo la hipotenusa es 13 y uno de los catetos es 12. Determina el valor de la cotangente del ángulo opuesto al lado menor.

Resolución:

Para hallar el menor lado de este triángulo podemos aplicar el teorema de Pitágoras.

⇒ x² = 13² – 12²
⇒ x = 5

Nos piden: «Cotθ»

∴ Cotθ = 12/5

VALORES DE LAS RAZONES TRIGONOMÉTRICAS DE LOS ÁNGULOS NOTABLES

Las razones trignométricas (seno, coseno, tangente…) aparecen muchísimas veces en Matemáticas relacionadas a cualquiera de sus ramas. Y en muchas ocasiones estamos obligados a calcular el valor de ellas en ciertos ángulos. Los que más suelen aparecer son estos 5 (los pongo en radiantes con su equivalencia en grados):

Estos ángulos son los más característicos del primer cuadrante. Ahora lo que nos interesa es saber cuáles son los valores del seno, del coseno y de la tangente de estos ángulos (los de los ángulos característicos de los otros cuadrantes pueden obtenerse a partir de ellos).

Razones trigonométricas de 30º y 60º

La altura divide al triángulo equilátero en dos triángulos rectángulos iguales cuyos ángulos miden 90º, 60º y 30º.

Si aplicamos el teorema de Pitágoras obtenemos la altura en función del lado:

Razones trigonométricas de 45º

La diagonal divide al cuadrado en dos triángulos rectángulos iguales cuyos ángulos miden 90º, 45º y 45º.

Si aplicamos el teorema de Pitágoras obetenemos la diagonal en función del lado:

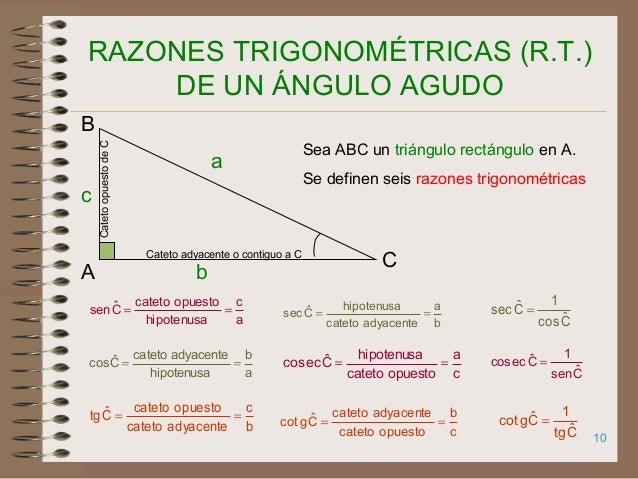
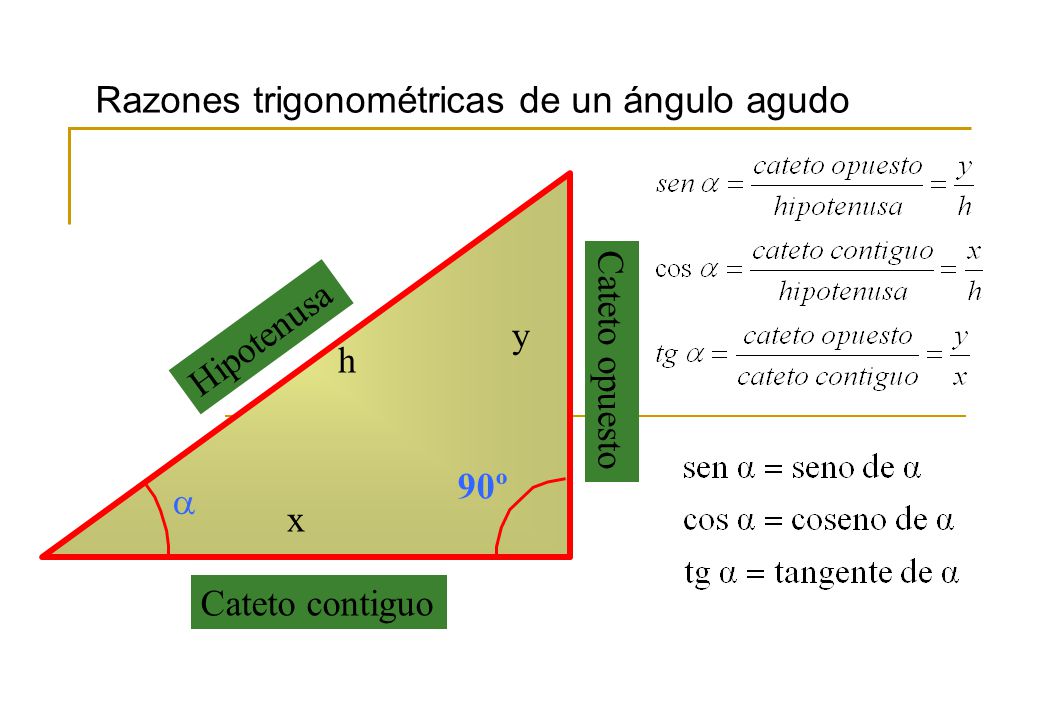
RESOLUCION DE TRIANGULOS RECTANGULOS

Los triángulos son polígonos que cuentan con tres lados. Cabe recordar que los polígonos son figuras planas, delimitadas por segmentos (es decir, por sus lados). El triángulo, por lo tanto, es una figura plana formada por tres segmentos.

Cuando un triángulo dispone de un ángulo recto (que mide noventa grados), se lo clasifica como un triángulo rectángulo. Los otros dos ángulos del triángulo rectángulo siempre son agudos (miden menos de noventa grados).

El ángulo recto en el triángulo rectángulo está formado por los dos lados de menor longitud, conocidos como catetos, mientras que el tercer lado (el de mayor extensión) recibe el nombre de hipotenusa. Las propiedades de estos triángulos señalan que la longitud de la hipotenusa siempre resulta menor que la suma de los catetos. La hipotenusa, por otra parte, siempre es más extensa que cualquiera de los dos catetos.

En la resolución de triángulos rectángulos nos encontramos 4 casos:

1 Se conocen la hipotenusa y un cateto:

  

Ejemplo:Resolver el triángulo conociendo:

a = 415 m y b = 280 m.

sen B = 280/415 = 0.6747     B = arc sen 0.6747 = 42° 25′

C = 90° - 42° 25′ = 47° 35′

c = a cos B   c = 415 · 0.7381 = 306. 31 m

2 Se conocen los dos catetos:

  Ejemplo:

Resolver el triángulo conociendo:

b = 33 m y c = 21 m

tg B = 33/21 = 1.5714      B = 57° 32′

C = 90° − 57° 32′ = 32° 28′

a = b/sen B   a = 33/0.8347 = 39.12 m

3 Se conocen la hipotenusa y un ángulo agudo:

  

Ejemplo:

Resolver el triángulo conociendo:

a = 45 m y B = 22°.

C = 90° - 22° = 68°

b = a sen 22°    b = 45 · 0.3746 = 16.85 m

c = a cos 22°     c = 45 · 0.9272 = 41.72 m

4 Se conocen un cateto y un ángulo agudo:

  

Ejemplo:

Resolver el triángulo conociendo:

b = 5.2 m y B = 37º

C = 90° - 37° = 53º

a = b/sen B     a = 5.2/0.6018 = 8.64 m

c = b · cotg B   c = 5.2 · 1.3270 = 6. 9 m