ÁNGULOS Y TRIÁNGULOS
ÁNGULOS
El ángulo está formado por la unión de dos rayos que tienen el origen común al que se llama vértice del ángulo, donde los rayos son los lados del mismo.
Un ángulo puede denotarse por el símbolo 
.Cuando dos ángulos se pueden superponer haciendo coincidir sus vértices y sus lados, decimos que los dos ángulos son iguales.
.Cuando dos ángulos se pueden superponer haciendo coincidir sus vértices y sus lados, decimos que los dos ángulos son iguales.
Ejercicio contextual:Mide los ángulos con el transportador y anota los resultados que obtengas.
Responde a estas cuestiones
- ¿Cuántos ángulos diferentes hay?
son 12 ángulos diferentes
- ¿Necesitaste medirlos todos?9
Vídeo de apoyo:
SISTEMAS DE MEDICIÓN
Medidas de ángulos. se considera al ángulo como resultado de un movimiento de rotación en el que una semirrecta gira alrededor de su origen y recorre el plano hasta coincidir con la otra semirrecta.
Para medir un ángulo se usa un instrumento llamado transportador, que generalmente tiene forma de semicírculo dividido en 180 unidades iguales llamadas grados (°).
La mayoría de los transportadores tiene la escala 0 a 180° marcada en dos direcciones del arco.
El uso adecuado del transportador requiere que:
- El centro del instrumento coincida con el diámetro señalado por la linea 0° - 180°
- La lectura se haga en la escala cuyo cero está sobre un lado del ángulo
- Si el instrumento resulta grande para la medición del ángulo, se prolongan los lados de éste.
Ejercicio: cuanto es la medida del ángulo "a" ?
PO:180- 46- 85= 49
R: 49°
CLASIFICACIÓN
Por su abertura
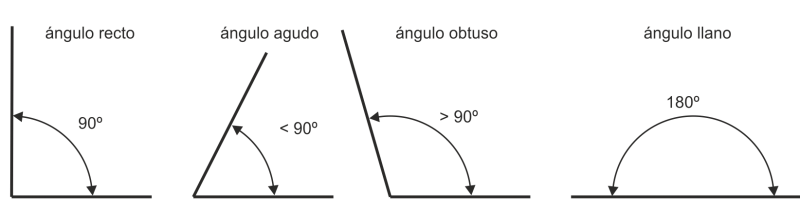
Clasificación de ángulos. según su amplitud, los ángulos se clasifican como: agudo, recto, obtuso y llano.
Ángulo agudo: es aquel cuyo valor es menor de 90°
Ángulo recto: es aquel cuyo valor es de 90°
Ángulo obtuso: es aquel cuyo valor es mayor de 90°, pero menor de 180°
Ángulo llano: su valor es de 180°, también se llama ángulo de lados colineales, porque sus lados están situados sobre una misma linea recta
Ángulo convexo: su medida es menor que un cuarto de vuelta es decir, menor que 90°
Ángulo cóncavo: es aquél cuya medida es mayor que media vuelta pero menor que una vuelta, es decir, mayor que 180° pero menor que 360°
Por la posición de sus lados
Ángulos opuestos por el vértice. son ángulos cuyo lados forman dos pares de rayos opuestos
Ejercicio: con base de los datos de la siguiente figura, calcula el valor de los ángulos que se indican en cada caso.
RECTAS PARALELAS CORTADAS POR UNA TRANSVERSAL
Dos paralelas cortadas por una transversal forman ocho ángulos, cuatro llamados internos, por estar situados dentro de las paralelas y cuatro llamados externos, por estar fuera de ellas.
Se llaman ángulos correspondientes a los ángulos situados del mismo lado de la trasversal.
Se llaman ángulos alternos internos los ángulos situados a uno y a otro lado de la transversal (alternos) y dentro de las paralelas (internos).
Se llaman ángulos alternos externos a dos ángulos situados a uno y a otro lado de la transversal (alternos) y fuera de las paralelas (externos)
Se llaman ángulos colaterales internos a dos ángulos situados en el mismo lado de la transversal (colaterales) y dentro de las paralelas (internos)
Se llaman ángulos colaterales externos a dos ángulos situados del mismo lado de la transversal (colaterales) y y fuera de la paralelas (externos)
Ejercicio:En la siguiente figura identifica los pares de los ángulos que son correspondientes, alternos internos, alternos externos, colaterales internos, colaterales externos.
TRIÁNGULOS
Un triángulo lo podemos entender como la unión de tres segmentos determinados por tres puntos no coloniales. Estos tres puntos se denominan vértices, y los segmentos, lados del triángulo; además, se determinan tres ´ángulos, cuyos lados son los lados del triángulo, y se denominan ´ángulos interiores del triángulo Se acostumbra usar letras minúsculas para los lados, de acuerdo al vértice al que se oponen.
Ejercicio: calcula "X"
Solución:En el triángulo ABC vemos dos ángulos externos conocidos, entonces podemos conocer el ángulo externo del ángulo «B».
Por propiedad de suma de ángulos externos:
130° + 145° + α = 360°
⇒ α = 85°
⇒ α = 85°
En «B»:
⇒ x + 85° = 180°
∴ x = 95°
∴ x = 95°
Vídeo de apoyo:
CLASIFICACIÓN Y SUS PROPIEDADES
Los triángulos se clasifican según sus lados y sus ángulos.
Por la medida de sus lados
Triángulo escaleno: es aquel que no tiene lados iguales
Triángulo isósceles: es aquel que no tiene por lo menos dos lados iguales
Triángulo equilátero: es aquel que tiene sus lados iguales
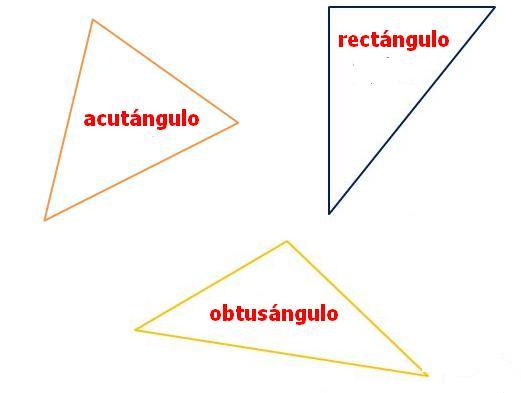
Por la abertura de sus ángulos
Triángulo rectángulo: es aquel que tiene un ángulo recto. Los lados que forman el ángulo recto se llaman catetos y el lado opuesto a dicho ángulo se llama hipotenusa.
Triángulo obtusángulo:es aquel que tiene un ángulo obtuso
Triángulo acutángulo: es el que tiene sus tres ángulos agudos
RECTAS Y PUNTOS NOTABLES
Mediatriz de un lado de triángulo es la recta perpendicular a ese lado en su punto medio.
Mediana de un triángulo es el segmento de recta que une un vértice con el punto medio del lado opuesto
Bisectriz de un ángulo en general y de un ángulo de un triángulo en la semirrecta que biseca el ángulo, es decir, divide el ángulo en dos ángulos congruentes.
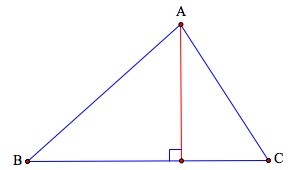
Altura de un triángulo es el segmento de recta perpendicular que se traza desde un vértice al lado opuesto
Circunferencia. es el punto de intersección de las mediatrices de los lados de un triángulo
Baricentro en el punto de intersección de las medianas de un triángulo. El baricentro es el centro de gravedad, es decir, el punto donde está aplicando todo el peso de un cuerpo de forma triangular cuya masa está uniformemente distribuida; de tal manera que el cuerpo estará en equilibrio si se apoya en el baricentro.
Incentro es el punto de intersección de las bisectrices de los ángulos interiores del triángulo.
Ortocentro es el punto de intersección de las alturas de un triángulo.
Ejercicio:construye una mediatriz una mediana en un triángulo dado.
SEMEJANZAS Y CONGRUENCIA
Se llaman triángulos semejantes a los triángulos que tienen sus ángulos respectivamente congruentes y sus lados homólogos son proporcionales.
La relación de semejanzas se denota con el simbolo ~, de esta manera la expresión ABC~ A'B'C' se lee: "el triángulo ABC es semejante al triángulo A prima, C prima".
Tres lados proporcionales L L L
Dos triángulos son semejantes si tienen sus tres lados respectivamente proporcionales (lado- lado- lado)
L A L
Dos triángulos son semejantes si tienen respectivamente congruentes un ángulo comprendido entre lados proporcionales (lado- ángulo-lado).
A L A
Dos triángulos son semejantes si tienen un lado proporcional comprendido entre dos ángulos congruentes.
congruencia: figuras congruentes son aquellas que tienen la misma forma y el mismo tamaño, de manera que al colocar una sobre la otra coinciden en sus partes correspondientes.
Dos triángulos son iguales si al colocar uno sobre otro coinciden en todas sus partes.
Los triángulos congruentes tienen la misma forma e igual al tamaño.
Criterios de congruencia
Ejercicio:En la siguiente figura determinar el
valor del segmento AB
Solución:
TEOREMA DE TALES
EL teorema de Tales se considera el teorema fundamental de la semejanza de triángulos y establece lo siguiente:
Toda recta paralela a un lado de un triángulo, forma con los otros dos lados o con sus prolongaciones otro triángulo que es semejante al triángulo dado.
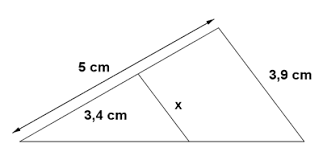
Ejercicio:determina la medida de los lados cuyo valor se desconoce.
TEOREMA DE PITÁGORAS
Hace años, un hombre llamado Pitágoras descubrió un
hecho asombroso sobre triángulos:
Si el triángulo tiene un ángulo recto (90°)...
... y pones un cuadrado sobre cada uno de sus lados, entonces...
... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!
El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados
(llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)
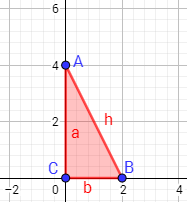
Ejercicio:En el siguiente triángulo,
¿cuál de los lados es la hipotenusa y cuál es el ángulo
recto?
solución:Los catetos son los lados
y . La hipotenusa es el lado . El ángulo recto es el ángulo que forman ambos catetos.
Para calcular la longitud de la hipotenusa, aplicamos Pitágoras. Los catetos miden y , con lo que
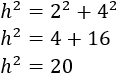
Finalmente, hacemos la raíz cuadrada:
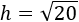
Simplificamos el resultado escribiendo el radicando como un producto y aplicando la propiedad de que la raíz de una producto es el producto de las raíces de sus factores:
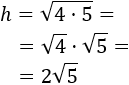
Si aproximamos, .
BLOQUE 2 PROPIEDADES DE LOS POLÍGONOS
POLÍGONOS
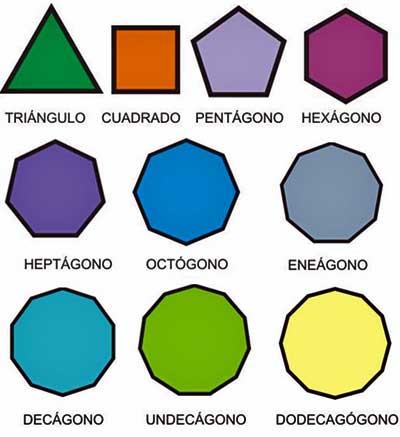
Polígono es la figura plana delimitada por una poligonal cerrada donde los segmentos son los lados del polígono y los puntos de intersección de los segmentos son los vértices se designan con letras mayúsculas en orden alfabético. Los polígonos se nombran de acuerdo con su número de lados, así tenemos que: triángulos, cuadrilátero, pentágono, hexágono, heptágono, octágono, eneágono, decágono, dodecágono, e icoságono, son poligonos de 3,4,5,6,7,8,9,10,12 y 20 lados, respectivamente.
Para nombrar a los demás polígonos se indica el número de los lados que tienen: polígonos de 17 lados, polígonos de 25 lados, etcétera.
Para nombrar un polígono se nombran sus vértices en forma ordenada según el giro de las manecillas de reloj, o bien, en sentido contrario.
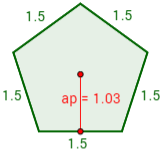
Ejercicio: Calcular el perímetro de un pentágono regular de lado 1.5cm y apotema 1.03cm.
Para calcular el perímetro sólo necesitamos saber la longitud de los lados. Como hay cinco lados y todos miden 1.5cm, el perímetro es
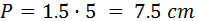Por tanto, el perímetro del pentágono es 7.5cm.
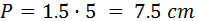
vídeo de apoyo:
ELEMENTOS Y SU CLASIFICACIÓN
Polígonos regulares es aquel que es un equilátero y equiángulo, es decir, tiene sus lados iguales y sus ángulos iguales.
Un polígono es regular cuando es equilátero y equiángulo, es decir, sera polígono regular cualquiera que cumpla las dos condiciones.
Los seis primeros polígonos regulares son:
El centro de un polígono regular es el centro de su circunferencia circunscrita. Si el centro de un polígono regular se une con todos sus vértices, a cada lado se pondrá un ángulo que se llama ángulo central.
Polígono irregular es aquel que no cuenta con las dos características que distinguen a un polígono regular, es decir, no tienen sus lados y ángulos iguales.
Los cuadriláteros se clasifican, por la disposición relativa de sus lados, en paralelogramos, trapecios y trapezoides.
Paralelogramo es el cuadrilátero que tiene paralelos sus lados opuestos y al cual se le llama también romboide.
Son paralelogramos el rectángulo, el rombo y el cuadrado.
Rectángulo es el paralelogramo que tiene un ángulo recto. por la forma en la que se ha definido, sabemos que el rectángulo tiene todas sus propiedades del paralelogramo, en particular la 3 y 4 aseguran que los cuatro ángulos son rectos.
Rombo es el paralelogramo que tiene dos lados consecutivos iguales.
Ejercicio: si ABCD es un rombo, halla X y Y
Solución:
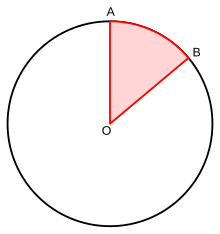
ÁNGULO CENTRAL
El centro de un polígono regular es el centro de su circunferencia circunscrita. Si el centro de un polígono regular se une con todos sus vértices, a cada lado se opondrá un ángulo que se llama ángulo central.
El centro del polígono es O. Es un ángulo central AOB.
ÁNGULO INTERIOR
Dos lados consecutivos de un polígono regular forman un ángulo interior.
ÁNGULO EXTERIOR
En un polígono si se prolongan sus lados en un mismo sentido, se forman entre estas prolongaciones y los lados del polígono ángulos a los que se llama exteriores.
SUMA DE ÁNGULOS CENTRALES, INTERIORES Y EXTERIORES
En un polígono regular la suma de sus ángulos centrales es igual a 360°, y como todos ellos miden lo mismo, porque son congruentes, la medida de uno cualquiera se obtiene dividiendo 360° entre el número de ángulos centrales que es igual al número de lados n del polígono.
Suma de ángulos interiores:
suma de ángulos interiores de polígonos regulares. Sabemos que la suma de los ángulos interiores de un triángulo es igual a 180°
Suma de ángulos interiores:en un polígono regular, para un vértice cualquiera, los ángulos interior y exterior son suplementarios.
Si el número de los lados de un polígono regular es n, entonces tendrá n vértices y habrá n pares de ángulos adyacentes suplementarios.
Por lo tanto, la suma S de los pares de ángulos adyacentes suplementarios en un polígono regular de n lados será:
S=180°
Ejercicio: calcula la medida del ángulo central de un pentágono regular.
Solución:
DIAGONALES
En un polígono se llama diagonal al segmento de recta que une dos vértices no consecutivos. Un triángulo no tiene diagonales, pues dos vértices cualesquiera son necesariamente consecutivos.
Si en un polígono se traza desde un soló vértice todas las diagonales es igual al número de lados menos 3; de manera que para un polígono de n lados el número de diagonales trazadas desde un vértice es n~ 3.
Ejercicio:calcula el número de diagonales que se pueden trazar en un hexágono
Respuesta: n=6
PERÍMETROS Y ÁREAS
El perímetro de los triángulos ya ha sido tratado, por lo que ahora se verá lo relacionado con el perímetro de algunos cuadriláteros en particular y de los polígonos regulares en general.
Perímetro del rectángulo
El perímetro del rectángulo se obtiene multiplicando por dos la suma de su ancho y su largo (es decir, base más altura).
P= a+b+a+b
P= a+b+a+b
P= 2a + 2b
P= 2(a+b)(formula)
P= 2(a+b)(formula)
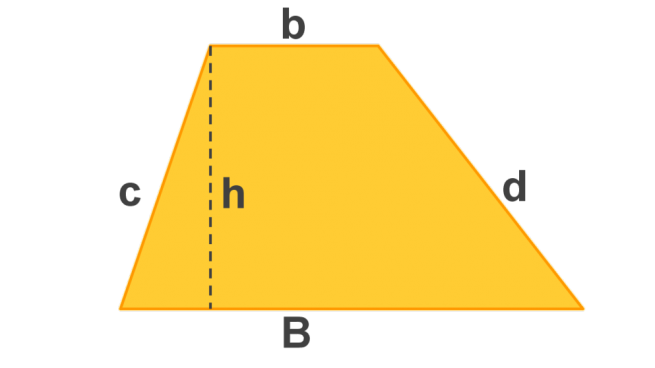
PERÍMETRO DEL TRAPECIO
El perímetro del trapecio se obtiene sumando lo que miden sus cuatro lados.
P= a+b+c+d(formula)
Área:El área de una superficie es el número de unidades cuadradas o fracciones de ella que contiene.
ÁREA DEL CUADRADO:
El área de un cuadrado se obtiene elevando al cuadrado la longitud de uno de sus lados.
Si la longitud del lado es a el área A es: A = a2
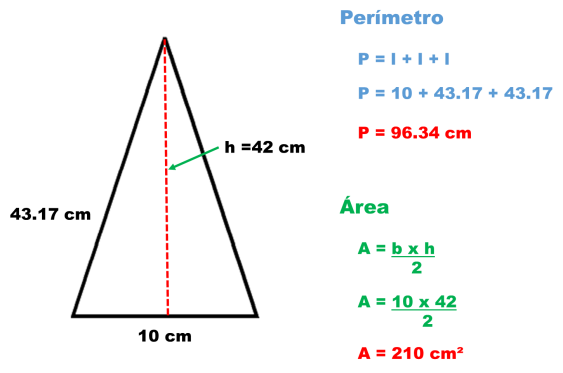
Ejercicio:Calcula el área y perímetro de un triángulo cuya base mide 10 cm, su lado 43.17 cm y su altura 42 cm
POLIEDROS
Los cuerpos o sólidos geométricos están limitados por superficies planas, por superficies planas o curvas o únicamente por superficie curva.
Los sólidos geométricos que están limitados por superficies planas se les llama poliedros, algunos ejemplos de poliedros son el cubo o hexaedro y el paralelepípedo rectángulo.
Elementos y clasificación
En un poliedro se pueden observar caras planas, aristas, vértices, ángulos planos, ángulos diedros, y ángulos sólidos o ángulos poliedros.
- Las caras de un poliedro son las superficies planas que lo limitan.
- Las aristas son las intersecciones de cara par de caras.
- Los vértices son las intersecciones de los aristas.
- Los ángulos planos se forman entre cada dos aristas concurrentes.
- Los ángulos dietros se forman entre cada dos caras contiguas.
- Los ángulos sólidos o ángulos poliedros se forman entre las caras que se intersecan en un mismo vértice.
Solamente hay cinco poliedros regulares
- Tetraedro
- hexaedro (cubo)
- Octaedro
- dodecaedro
Icosaedro
Ejercicio:Calcula el número de vértices de un poliedro convexo, si la suma de las medidas de los ángulos internos de todas las caras es 1140°
Solución:
Por dato: S caras=1440°
360°(V - 2)=1440°----> V_2=6 -----> V=8
VOLÚMENES
El volumen de un cubo se obtiene multiplicando el área de la base, por su altura. Como las caras que limitan al cubo son cuadrados, entonces el área de las bases corresponde al área del cuadrado que se obtienen multiplicando lado por lado.
No hay comentarios.:
Publicar un comentario