ELEMENTOS DE LA CIRCUNFERENCIA
3.1 Circunferencia y círculo
Es común que se utilicen circunferencia y círculo como sinónimos, sin embargo, aún cuando estos conceptos están estrechamente vinculados, tienen significados que es preciso distinguir para poder aplicarlos correctamente.
Ejercicio 2.
Hallar «x», si «O» es centro de la circunferencia.
Trazamos el radio OB para formar el angulo central en la circunferencia.
– Por ángulo central: m∡AOB = arco AB = 140°.
El triángulo AOB es triángulo isósceles entonces trasladamos el ángulo «x».
Por último, en el triángulo AOB aplicamos propiedad de suma de ángulo internos:
⇒ x + x + 140 = 180°∴ x = 20°
Ejercicio 03:
Área del sector circular A=πr2 ∞ ------------ 360°Área de la corona circular A=π (R2 - r2)Área del trapecio circular A=π (R2 - r2) ∞ ---------------- 360°Área del semicírculo A= πr2 ---------------- 2Área del segente circular A= πR2 0 - R2 - sen 0 =R2 (0 - sen 0)----------------------------- 360° 2 2
Área de regiones sombreadas
Concepto de circulo y circunferencia
La circunferencia es una curva cerrada cuyos puntos están en un mismo plano y a igual distancia de otro punto interior que se llama centro de la circunferencia.
El circulo es la superficie del plano limitado por una circunferencia.
La circunferencia o circulo se representa con el símbolo ○ y la diferencia se obtiene del contexto.
El concepto de π se aplica en la transformación de medidas angulares.
Segmentos y rectas de la circunferencia
Dentro de los elementos de la circunferencia de dan a conocer las líneas notables
AB - Cuerda
CD - Diámetro
EF - Secante
GH - Tangente
OI - Radio
Radio: es el segme4nto de recta que une el centro de la circunferencia con un punto cualquiera de la misma.
Diámetro: Es la cuerda que pasa por el centro de la circunferencia
Cuerda: Es el segmento de recta que une a dos puntos de la circunferencia
Arco: Es una parte de la circunferencia.
Tangente: Es la recta que toca a la circunferencia en un punto. Este punto se le llama punto de tangencia o punto de contacto.
Secante: Es la recta que corta a la circunferencia en dos puntos o partes.
Semicircunferencia: Es el arco de longitud igual a la mitad de la circunferencia.
Arco menor: Es aquel que mide menos que una semicircunferencia.
Arco mayor: Es aquel que mide más que una semicircunferencia.
Semicírculo: Es la región del plano conoprendida entre un diámetro y la semicircunferencia correspondiente.
Rectas tangente a un círculo
Construye la tangente a una circunferencia dada en un punto determinado de ella.
Sean la circunferencia 0 y un punto P de ella.
1. Traza y prolonga el radio OP
2.En P se aplica la primera construcción y se determina AB.
AB es la recta tangente a la circunferencia 0 en el punto P, que es el punto de tangencia.
Observa que la radio es perpendicular a la tangente en el punto de tangencia.
Construye una tangente a una circunferencia dada desde un punto exterior a ella.
Sean la circunferencia 0 y un punto P exterior a ella.
1. Traza el segmento OP.
2. Se determina el punto medio OP.
3. Con centro en M y radio OM, traza una circunferencia que corre a la circunferencia dada en los puntos A y B.
4. Traza las rectas PA y PB, que son las tangentes a la circunferencia dada.
Ejercicio :
Hallar las tangentes a la circunferencia x2 + y2 - 2x + 3y - 18 = 0 por los puntos (2, 3), (1, 1) y (5, 5).

 es:
es:  La pendiente de la tangente es:
La pendiente de la tangente es: 
 · En el caso del punto (5, 5) hay que hallar las rectas que, conteniendo a éste, su distancia al centro es el radio.
· En el caso del punto (5, 5) hay que hallar las rectas que, conteniendo a éste, su distancia al centro es el radio.
 La ecuación de una recta que contenga a (5, 5) es y - 5 = m( x - 5) Þ
La ecuación de una recta que contenga a (5, 5) es y - 5 = m( x - 5) Þ



 169 - 208m + 64m2 = 85 + 85m2 21m2 + 208m - 84 = 0
169 - 208m + 64m2 = 85 + 85m2 21m2 + 208m - 84 = 0
 La pendiente de la tangente es:
La pendiente de la tangente es: 


Angulos en la circunferencia
En el caso de los angulo notables se muestran los teoremas con los cuales se reducen en las formulas para calcular sus respectivas medidas.
Angulo central: Es aquel que está formado por dos radios.
Angulo inscrito : Es aquel que está formado por dos cuerdas y tiene su vértice sobre la circunferencia.
Angulo interior: Es aquel que está formado por dos cuerdas que se cortan.
Angulo exterior: Es aquel que está formado segmentos secantes que se cortan en un punto fuera del círculo.
Ejercicios:
Calcular X en la figura si (A) y (B) son puntos de tangencia
Solución:
En este ejercicio utilizaremos las formulas del ángulo inscrito y exterior de las circunferencias
Por ángulo inscrito: Arco AB = 2(60°) = 120°Por ángulo exterior: x + 120° = 180°
∴ x = 60°
En este ejercicio utilizaremos las formulas del ángulo inscrito y exterior de las circunferencias
Por ángulo inscrito: Arco AB = 2(60°) = 120°Por ángulo exterior: x + 120° = 180°
∴ x = 60°
Ejercicio 2.
Hallar «x», si «O» es centro de la circunferencia.
Solución:
Trazamos el radio OB para formar el angulo central en la circunferencia.
– Por ángulo central: m∡AOB = arco AB = 140°.
El triángulo AOB es triángulo isósceles entonces trasladamos el ángulo «x».
Por último, en el triángulo AOB aplicamos propiedad de suma de ángulo internos:
⇒ x + x + 140 = 180°∴ x = 20°
Ejercicio 03:
En la Figura mostrada Calcular el valor de «x» si A, B, C y E son puntos de tangencia. Solución:
Solución:
Este ejercicio no es necesariamente de ángulos en la circunferencia, pero nos ayudará a conocer cómo se aprovechan las rectas tangentes a la circunferencia. Veamos:
ΔADB: Triángulo Isósceles, también lo es el triángulo EDC. Vea la siguiente figura:
Δ BPE: Por propiedad del triángulo, tenemos:
x =α + θΔ PAC, Se cumple:
2α + 2θ = 180
⇒ α + θ = 90° = x
∴ x = 90°En la Figura mostrada Calcular el valor de «x» si A, B, C y E son puntos de tangencia. Solución:Este ejercicio no es necesariamente de ángulos en la circunferencia, pero nos ayudará a conocer cómo se aprovechan las rectas tangentes a la circunferencia. Veamos:
Solución:Este ejercicio no es necesariamente de ángulos en la circunferencia, pero nos ayudará a conocer cómo se aprovechan las rectas tangentes a la circunferencia. Veamos:
ΔADB: Triángulo Isósceles, también lo es el triángulo EDC. Vea la siguiente figura:
Δ BPE: Por propiedad del triángulo, tenemos:
x =α + θΔ PAC, Se cumple:
2α + 2θ = 180
⇒ α + θ = 90° = x
∴ x = 90°
 Solución:
Solución:Este ejercicio no es necesariamente de ángulos en la circunferencia, pero nos ayudará a conocer cómo se aprovechan las rectas tangentes a la circunferencia. Veamos:
ΔADB: Triángulo Isósceles, también lo es el triángulo EDC. Vea la siguiente figura:

Δ BPE: Por propiedad del triángulo, tenemos:
x =α + θΔ PAC, Se cumple:
2α + 2θ = 180
⇒ α + θ = 90° = x
∴ x = 90°En la Figura mostrada Calcular el valor de «x» si A, B, C y E son puntos de tangencia.
 Solución:Este ejercicio no es necesariamente de ángulos en la circunferencia, pero nos ayudará a conocer cómo se aprovechan las rectas tangentes a la circunferencia. Veamos:
Solución:Este ejercicio no es necesariamente de ángulos en la circunferencia, pero nos ayudará a conocer cómo se aprovechan las rectas tangentes a la circunferencia. Veamos:ΔADB: Triángulo Isósceles, también lo es el triángulo EDC. Vea la siguiente figura:

Δ BPE: Por propiedad del triángulo, tenemos:
x =α + θΔ PAC, Se cumple:
2α + 2θ = 180
⇒ α + θ = 90° = x
∴ x = 90°
Medida del angulo central
Un ángulo central se mide por el arco comprendido entre sus lados.
La unidad para medir los ángulos es el grado que, como ya se ha dicho, equivale a la amplitud de rotación de una semirrecta que gira.
1
---
360
De vuelta alrededor de su origen.
1
---
360
De vuelta a unñ grado, unidad angular.
1
---
360
De circunferencia es un grado, unidad del arco.
La medida del ángulo central es igual a la del arco comprendido entre sus lados.
Ejercicios :
1. Obtener la longitud de un arco de circunferencia cuyo ángulo central mide 82° y su radio 3.41 cm.
Por lo tanto, la longitud del arco del ángulo central de 82° mide 4.876cm.2. Obtener la longitud de un arco de circunferencia cuyo ángulo central mide 50° y su radio 4 cm.
Por lo tanto, la longitud del arco del ángulo central de 50° mide 3.488cm.3. Obtener la longitud de un arco de circunferencia cuyo ángulo central mide 30° y su radio 8 cm.
Por lo tanto, la longitud del arco del ángulo central de 30° mide 4.186 cm.

Por lo tanto, la longitud del arco del ángulo central de 82° mide 4.876cm.2. Obtener la longitud de un arco de circunferencia cuyo ángulo central mide 50° y su radio 4 cm.

Por lo tanto, la longitud del arco del ángulo central de 50° mide 3.488cm.3. Obtener la longitud de un arco de circunferencia cuyo ángulo central mide 30° y su radio 8 cm.

Por lo tanto, la longitud del arco del ángulo central de 30° mide 4.186 cm.
Perímetro de la circunferencia
Se ha establecido que π es la razón entre la longitud de la circunferencia y la longitud del diámetro, lo cual se expresa así:
π= C
---
d
Entonces C= d y como el diámetro es igual a dos radios (d=2r) C=2πr.
La longitud de un circunferencia se obtiene multiplicando π por la diámetro, o lo que es lo mismo π por el doble del radio.
Ejercicios:
1. Calcular la longitud de una circunferencia que mide 5 cm de radio.
2. Calcular la longitud de una circunferencia que mide 5 cm de diámetro.
Área del circulo
Considerado el circulo como un polígono regular de un número ilimitado de lados, el área del circulo se puede obtener aplicando la formula para los polígonos regulares.
A= PA
------
2
Solo que el perímetro del círculo es la longitud de la circunferencia (P=C=2 πr) y la apotema es igual al radio (a=r).
Por tanto:
A = PA
-----
2
A = (2 π r) (r)
---------------
2
A = 2 π r2
---------------
2
A = π r2
El área de un círculo se obtiene multiplicando π por el cuadrado del radio.
Ejercicios :
1.Calcular el área de un círculo que mide 5m de radio.
2. Calcular el área de un círculo si su circunferencia mide 18 Π.
Secciones de un círculo (Corona, Sector y Trapecio circular)
Semicírculo es la región del plano comprendida entre un diámetro y la semicircunferencia correspondiente.
Segmentos es la parte de circulo limitada entre una cuerda y su arco.
Sector es la parte de circulo limitada por dos radios y el arco correspondiente entre ellos.
Corona circular es el espacio del circulo limitado por dos circunferencias conconcéntricas .
Cuadrante circular es la parte de circulo limitada por dos radios perpendiculares y el arco correspondiente entre ellos.
Trapecio circular es la porción del plano limitada por dos circunferencias concéntricas y dos radios.
Área del círculo A=π r2
Área del sector circular A=πr2 ∞ ------------ 360°Área de la corona circular A=π (R2 - r2)Área del trapecio circular A=π (R2 - r2) ∞ ---------------- 360°Área del semicírculo A= πr2 ---------------- 2Área del segente circular A= πR2 0 - R2 - sen 0 =R2 (0 - sen 0)----------------------------- 360° 2 2
Ejercicios: 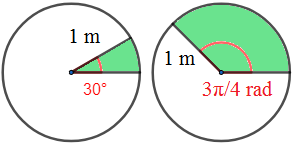
1.Calcular el área del sector circular de una circunferencia de radio 1 metro y ánguloPara el ángulo en grados utilizamos la fórmula
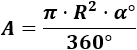
Sustituimos los datos:
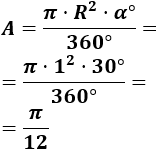
El área del sector circular es . Es decir, aproximadamente, .Para el ángulo en radianes utilizamos la fórmula
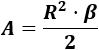
Sustituimos los datos:
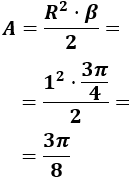
El área del sector circular es . Es decir, aproximadamente, .
2.Calcular en grados y en radianes el ángulo del sector circular con área igual a de un circulo cuyo perímetro es .
Calculamos el radio del círculo a partir de su perímetro ():
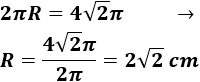
Vamos a utilizar la fórmula del área de un sector circular con el ángulo expresado en radianes:
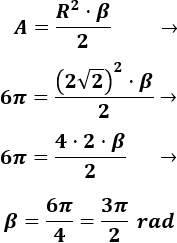
El ángulo del sector es . En grados, el ángulo es .
Área de regiones sombreadas
Cálculo de figuras sombreadas
Área de la región 1.
Área del cuadrado - área del sector
Área de regiones 2y3
Área de semicírculo - 1
---
2
área del cuadrado
Radio del semicírculo
Descripciónj
Descripción
Área de la región sombreada = área que + área 2 + área 3.
Cómo se puede observar, el área de la región sombreada corresponde a la suma de las áreas de la región 1, 2 y 3.
el área de la región uno se puede obtener restando el área del cuadrado de lado 4 ,el área del cuadrante circular de radio 4.
El área de las regiones 2 y 3 se puede obtener calculando el radio del semicírculo que tiene como diámetro a la diagonal del cuadrado
Después el área del semicírculo se le puede restar el área de la mitad del cuadrado.
Radio del semicírculo
La medida de la diagonal (d) se puede calcular utilizando el teorema de Pitágoras, por lo que:
Por lo que el radio mide la mitad de la diagonal, esto es:
2√2 cm r
De acuerdo con lo anterior ,el área de la semicircunferencia es:
Descripción
Descripción
Descripció
Descripci
Descripciónπ (4cm) 2
Entonces el área de la región 2 y 3 = a:
El área de la región sombreada es igual a la suma de las áreas de las regiones
1, 2 y 3 ,es decir:
Efectuando operaciones:
=8 cm2
Ejercicios:
1. Calcular el área de la región sombreada donde r = 2 cm
▪ cálculo del área del circulo
▪ cálculo del área del cuadrado
▪ cálculo del área de la región sombreada = área del cuadrado área -del círculo
2. Calcular el área de la región sombreada (sector circular) donde r = 3 cm
▪ Cálculo del ángulo 0
▪ Cálculo del área del sector circular
A= Π r2 0
--------
360°
3. Calcular el área de la región sombreada (corona circular) donde r1=5cm y r2 = 3 cm
▪ Cálculo del área del circulo de radio r1
▪ Cálculo del área del circulo de radio r2
▪ Cálculo del área de la corona circular = área del circulo de r1 - área del circulo r2.
4. Calcular el área de la región sombreada (trapecio circular) donde r1 = 5 cm y r2 =4cm.
▪Cálculo del sector circular del radio r1.
▪ Cálculo del sector circular del radio r2.
▪ Cálculo del trapecio circular = área del sector con r1 - área del sector con r2.
5. Calcular el área de la región sombreada si r=2 cm.










































